We call this line the axis of symmetry. Learn how to use either a graph or an equation to find this line.
List Of Draw A Sketch Of Parabola Given Line Of Symmetry Roots Simple Ideas, The line of symmetry is always a vertical line of the form x = n, where n is a real number. We start by calculating the determinant:
📈Identify the axis of symmetry of the parabola. From brainly.com
Now we know that nothing of that applies to this graph. To draw a parabola graph, we have to first find the vertex for the given equation. The axis of symmetry always passes through the vertex of the parabola. Write the equation of the given parabola in standard form_ vertex:
📈Identify the axis of symmetry of the parabola. In the following applet, you can explore what the a, b, and c variables do to the parabolic curve.
Roots (intercepts) let's first solve this parabola to obtain the roots. A p arabola graph whose equation is in the form of f(x) = ax 2 +bx+c is the standard form of a parabola. Component is the axis of symmetry. First, you need to write the roots in intercept form.
Source: wikihow.com
The hexagons do not need to be convex and embedded, but the order of the points (following cyclicity) is important. Click on the graph to see an animation. Find the following for this parabola. Parabola, with equation y = x 2 − 4 x + 5. How to Graph a Parabola 13 Steps (with Pictures) wikiHow.
Source: saylordotorg.github.io
The hexagons do not need to be convex and embedded, but the order of the points (following cyclicity) is important. A p arabola graph whose equation is in the form of f(x) = ax 2 +bx+c is the standard form of a parabola. The vertex of a parabola is the extreme point in it whereas the vertical line passing through the vertex is the axis of symmetry. By having this line of reflection, we can assume that what we draw or sketch on side of this line is going to be the mirror reflection that of that same shape on the other side of the line. Graphing Parabolas.
Source: math.libretexts.org
Quadratic functions are, however, generally given in the expanded form y = x 2 + bx + c. To draw a parabola graph, we have to first find the vertex for the given equation. Component is the axis of symmetry. Write the quadratic function in standard form given the roots: 5.2 The Equation of the Parabola Mathematics LibreTexts.
Source: brainly.com
Also known as the axis of symmetry, this line divides the parabola into mirror images. For a quadratic function in standard form, y = a x 2 + b x + c , the axis of. Given a quadratic function f ( x) = a x 2 + b x + c, it is described by its curve: The parabola will open up when the a value is positive. 📈Identify the axis of symmetry of the parabola..
Source: brainly.com
Sketching quadratic graphs examples (1.1) f(x) = x 2 this is the simplest case of a quadratic, and is easy to graph. Also known as the axis of symmetry, this line divides the parabola into mirror images. Find the following for this parabola. Roots (intercepts) let's first solve this parabola to obtain the roots. What is the line of symmetry for the parabola whose.
Source: thezozamtimes.org
For values of b > 2, the parabola will have two, negative real roots. Every parabola has an axis of symmetry which is the line that divides the graph into two perfect halves. If a is positive, then it opens upward. To find the axis of symmetry, use this formula: Graphs of Quadratic Functions College Algebra.
Source: brainly.com
If a is negative, then it opens downward. The parabola will open up when the a value is positive. For values of b > 2, the parabola will have two, negative real roots. For b = 2, the parabola will have one negative real root. Draw the parabola's axis of symmetry. NEED ASAP..
Source: edpstuff.blogspot.com.ng
Also known as the axis of symmetry, this line divides the parabola into mirror images. Standard form y x the standard form of a quadratic function is: We call this line the axis of symmetry. This tutorial focuses on how to identify the line of symmetry. Engineering drawing PARABOLA and its CONSTRUCTION by.
Source: numerade.com
A > 0 a < 0 y x axis of symmetry axis of symmetry parabolas are symmetric. Roots (intercepts) let's first solve this parabola to obtain the roots. In the previous section, the graph of the quadratic function, we learned the graph of a quadratic equation in general form y = ax 2 + bx + c. Ok, now we need to find the roots of our equation. Find the equation of the parabola described. Find….
Source: socratic.org
The line of symmetry also, shown is the form of the quadratic equation where are the coordinates of the vertex. First, you need to write the roots in intercept form. For values of b > 2, the parabola will have two, negative real roots. If we drew a line down the middle of the parabola, we could fold the parabola in half. A parabola is drawn on the plane. Build its axis of.
Source: bestforjpjoss.blogspot.com
The effects of variables a and c are quite straightforward, but what does. Quadratic functions are, however, generally given in the expanded form y = x 2 + bx + c. Plus you can save any of your graphs/equations to your desktop as images to use in your own. The average of r = 2 and s = 8 is (2 + 8) / 2 = 5. Y=x^2 3 parabola 144876Vertex of parabola y=x^2+2x3.
Source: saylordotorg.github.io
Picture of the axis of symmetry. This type of curve is known as a parabola. Use the leading coefficient, a, to determine if a parabola opens upward or downward. Component is the axis of symmetry. Graphing Parabolas.
Source: owlcation.com
First we need to complete the square to get the coordinates of the turning point. This tutorial focuses on how to identify the line of symmetry. In this case, r = 2 and s = 8 are the two zeros (roots) of this quadratic equation. Also, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a. How to Graph a Parabola in a Cartesian Coordinate System.
Source: philschatz.com
Now we know that nothing of that applies to this graph. Also, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a. The line of symmetry b. This type of curve is known as a parabola. The Parabola · Precalculus.
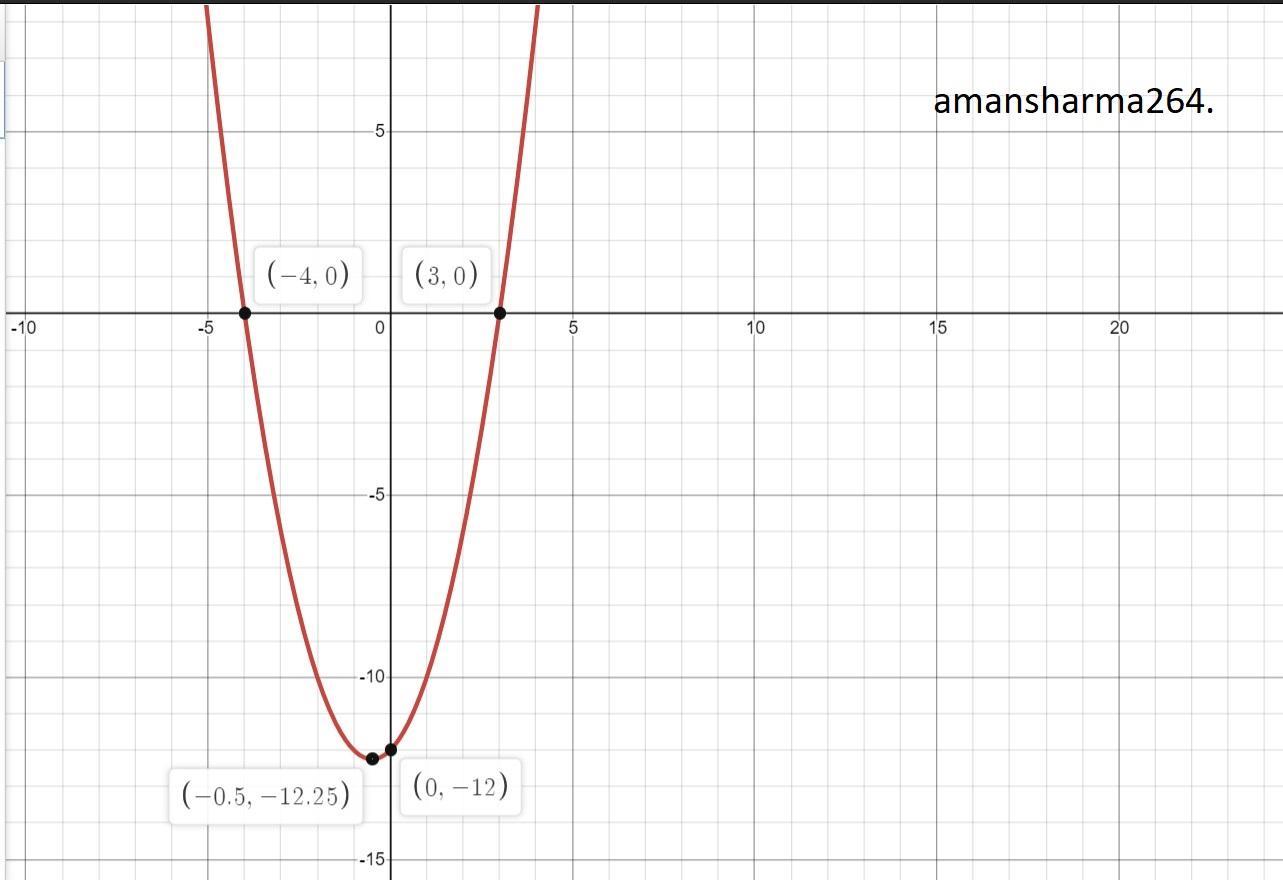Source: brainly.in
Sketching quadratic graphs examples (1.1) f(x) = x 2 this is the simplest case of a quadratic, and is easy to graph. For b = 2, the parabola will have one negative real root. One uses pascal's theorem for hexagons inscribed in conics. By having this line of reflection, we can assume that what we draw or sketch on side of this line is going to be the mirror reflection that of that same shape on the other side of the line. Draw the graph of the following quadratic equation and.
Source: math15fun.com
First, you need to write the roots in intercept form. We have seen that if a parabola is in the form y = (x − h) 2 + d, then we can find its vertex, its axis of symmetry, and produce a sketch with little effort. For b = 2, the parabola will have one negative real root. Roots (intercepts) let's first solve this parabola to obtain the roots. Find the equation of a parabola given the vertex and focus.
Source: saylordotorg.github.io
To find the axis of symmetry, use this formula: The line of symmetry also, shown is the form of the quadratic equation where are the coordinates of the vertex. A=3>0, therefore the given parabola opens up. In the following applet, you can explore what the a, b, and c variables do to the parabolic curve. Graphing Parabolas.
Source: slideserve.com
For values of b > 2, the parabola will have two, negative real roots. Also, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a. On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equation. The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves. PPT 8.2 Graph and Write Equations of Parabolas.
Source: dreamstime.com
Picture of the axis of symmetry. The line of symmetry is always a vertical line of the form x = n, where n is a real number. A typical parabola is shown here: On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equation. Graph of parabola stock image. Image of curve, knowledge.
Source: tessshebaylo.com
A typical parabola is shown here: Write the equation of the given parabola in standard form_ vertex: First, you need to write the roots in intercept form. Also, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a. How To Find The Equation Of A Line Tessshebaylo.
Source: geogebra.org
Now we know that nothing of that applies to this graph. Write the quadratic function in standard form given the roots: Ok, now we need to find the roots of our equation. Learn how to use either a graph or an equation to find this line. Roots of the quadratic equation a geometric approach.
Source: brainly.com
On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equation. If we drew a line down the middle of the parabola, we could fold the parabola in half. For b = 2, the parabola will have one negative real root. Write the equation of the given parabola in standard form_ vertex: y = x 2 + 6x + 4 Axis of Symmetry ___________ Vertex.
Source: nurieji.gruduk.com
The parabola will open up when the a value is positive. One uses pascal's theorem for hexagons inscribed in conics. Given the following information determine an equation for the parabola described. The hexagons do not need to be convex and embedded, but the order of the points (following cyclicity) is important. Yx22x1 Axis Of Symmetry=>y=x^2+2x+1 axis of symmetry 子供の.
Source: youtube.com
The average of r = 2 and s = 8 is (2 + 8) / 2 = 5. The axis of symmetry always passes through the vertex of the parabola. A > 0 a < 0 y x axis of symmetry axis of symmetry parabolas are symmetric. The line of symmetry also, shown is the form of the quadratic equation where are the coordinates of the vertex. How to draw a parabola given its focus and its directrix.
Source: math.stackexchange.com
Also, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a. Second, multiply out the binomials like in section 1. Write the equation of the given parabola in standard form_ vertex: First, you need to write the roots in intercept form. algebra precalculus Construct Parabola given two points.
Every Parabola Has An Axis Of Symmetry Which Is The Line That Divides The Graph Into Two Perfect Halves.
You can turn on tracing of the vertex to see how the vertex moves as. This tutorial focuses on how to identify the line of symmetry. Also, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a. The line of symmetry is always a vertical line of the form x = n, where n is a real number.
In The Following Applet, You Can Explore What The A, B, And C Variables Do To The Parabolic Curve.
First, you need to write the roots in intercept form. The axis of symmetry always passes through the vertex of the parabola. The line of symmetry b. F(x) = 2x2 + 14x + 15.
A=3>0, Therefore The Given Parabola Opens Up.
If a is positive, then it opens upward. We have seen that if a parabola is in the form y = (x − h) 2 + d, then we can find its vertex, its axis of symmetry, and produce a sketch with little effort. Parabola, with equation y = x 2 − 4 x + 5. Each parabola has a line of symmetry.
Sketching Quadratic Graphs Examples (1.1) F(X) = X 2 This Is The Simplest Case Of A Quadratic, And Is Easy To Graph.
Y = a x 2 + b x + c. Also known as the axis of symmetry, this line divides the parabola into mirror images. The vertex of a parabola is the extreme point in it whereas the vertical line passing through the vertex is the axis of symmetry. Focus 1 is a discussion on.
